attention 


Долгожитель
|
      
Цитата: sessia написал 31 авг. 2009 17:38
Помогите, пожалуйста, найти несобственный интеграл
int (от 1 до +беск.) 2^(x+1)/sqrt(x+1) dx
Никак не разберусь, с помощью дидактички смогла только:
int (от 1 до +беск.) 2^(x+1)/sqrt(x+1) dx =
lim (A->+беск.) 2^(x+1)/sqrt(x+1)
Задание исследовать ряд на сходимость Е (от n=1 до +беск.)2^(x+1)/sqrt(x+1) я решила через несобственный интеграл исследовать, может есть и легче способ...
sessia, просто попробуйте признак Даламбера; получите простой предел.
(Сообщение отредактировал attention 31 авг. 2009 18:08)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 31 авг. 2009 19:06 | IP
|
|
sessia


Новичок
|
     
спасибо, attention, сейчас попробую разобраться
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 31 авг. 2009 19:08 | IP
|
|
attention 


Долгожитель
|
      
Напишите, что у Вас получается, проверим.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 31 авг. 2009 19:09 | IP
|
|
sessia


Новичок
|
     
attention, пока не получилось... еще почитаю, порешаю, а потом к Вам за проверкой
(Сообщение отредактировал sessia 31 авг. 2009 20:11)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 31 авг. 2009 19:34 | IP
|
|
sessia


Новичок
|
     
attention, посмотрите, пожалуйста, я решала так:
lim (n->+беск.) |(2^(sqrt(n+1+1))/sqrt(n+1+1)) / (2^(sqrt(n+1))/sqrt(n+1))|=
=|(2^(sqrt(n+2))/sqrt(n+2))*(sqrt(n+1))/2^(sqrt(n+1))|=? а чему равняется не знаю
(Сообщение отредактировал sessia 1 сен. 2009 16:17)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 1 сен. 2009 15:41 | IP
|
|
attention 


Долгожитель
|
      
Цитата: sessia написал 31 авг. 2009 17:38
Помогите, пожалуйста, найти несобственный интеграл
int (от 1 до +беск.) 2^(x+1)/sqrt(x+1) dx
Никак не разберусь, с помощью дидактички смогла только:
int (от 1 до +беск.) 2^(x+1)/sqrt(x+1) dx =
lim (A->+беск.) 2^(x+1)/sqrt(x+1)
Задание исследовать ряд на сходимость Е (от n=1 до +беск.)2^(x+1)/sqrt(x+1) я решила через несобственный интеграл исследовать, может есть и легче способ...

Т.к. предел больше единицы, то, следовательно, ряд расходится по признаку Даламбера.
(Сообщение отредактировал attention 3 сен. 2009 17:21)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 1 сен. 2009 23:32 | IP
|
|
sessia


Новичок
|
     
attention, огромное Вам спасибо!
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 2 сен. 2009 15:50 | IP
|
|
Benzema18


Новичок
|
        
Помогите пожалуйста.
Выделив главные части на бесконечности либо в особой точке, исследовать на сходимость несобственные интегралы:


Заранее благодарен
(Сообщение отредактировал Benzema18 4 сен. 2009 22:22)
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 4 сен. 2009 22:05 | IP
|
|
Lyuda

Начинающий
|
       
Ребята... подскажите пожалуйста....
есть интеграл
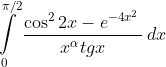
-- нужно найти значения параметра 
при которых интеграл сходится. в ответе стоит 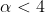
... а у меня < 2 получается....
(Сообщение отредактировал Lyuda 22 сен. 2009 21:10)
|
Всего сообщений: 73 | Присоединился: ноябрь 2007 | Отправлено: 22 сен. 2009 16:25 | IP
|
|
KrisRu

Новичок
|
     
Пожалуйста, помогите решить!

(Сообщение отредактировал KrisRu 27 сен. 2009 17:12)
|
Всего сообщений: 14 | Присоединился: сентябрь 2009 | Отправлено: 27 сен. 2009 17:11 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.11 Несобственные интегралы
2.1.11 Несобственные интегралы

 Форум
Форум

 Математика
Математика

 2.1.11 Несобственные интегралы
2.1.11 Несобственные интегралы