RKI 


Долгожитель
|
    
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
5) увавнение медианы А1 треугольника А1,А2,А3;
A1M - медиана треугольника A1A2A3.
Следовательно, точка M - середина стороны A2A3.
 )
 )
 )
 )
 )

Уравнение медианы A1M имеет вид:
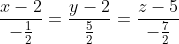
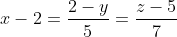
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 14:03 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
6) уравнение грани А1,А2,А3;
 )
 )
 )
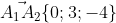
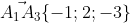
Уравнение грани A1A2A3 имеет вид:
|x-2 y-2 z-5| = 0
| 0 3 -4 |
| -1 2 -3 |
(x-2)*|3 -4| - (y-2)*|0 -4| + (z-5)*|0 3| = 0
|2 -3| |-1 -3| |-1 2|
(x-2)*(-9 + 8) - (y-2)*(0 - 4) + (z-5)*(0 + 3) = 0
- (x-2) + 4(y-2) + 3(z-5) = 0
- x + 2 + 4y - 8 + 3z - 15 = 0
- x + 4y + 3z - 21 = 0
x - 4y - 3z + 21 = 0
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 14:29 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Legenda написал 25 окт. 2009 10:34
Даны координаты вершин тетраэдра А1(2;2;5), А2(2;5;1), А3(1;4;2), А4(0;1;4). Найти:
7) уравнение высоты тетраэдра А4D, опущеной из вершины А4 на грань А1,А2,А3;
 )
Уравнение высоты A4D имеет вид:
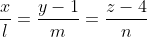
Уравнение плоскости A1A2A3 имеет вид:
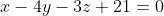
Прямая A4D и плоскость A1A2A3 перпендикулярны, следовательно,
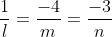
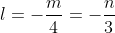
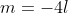
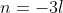
Таким образом, уравнение высоты A4D имеет вид:
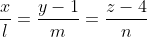
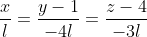
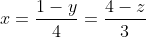
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 14:40 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Legenda написал 25 окт. 2009 10:34
8) длину высоты (двумя способами).
2 способ
 )
Точка D лежит на прямой A4D. Следовательно,
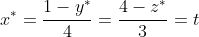
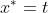
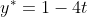
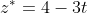
 )
С другой стороны точка D принадлежит плоскости A1A2A3. Следовательно,
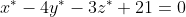
 - 3(4-3t) + 21 = 0 )
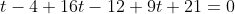

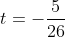
 )
 )
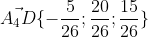
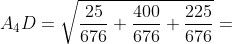
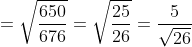
Как Вы видите первым и вторым способом получили один и тот же ответ
(Сообщение отредактировал RKI 25 окт. 2009 14:54)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 14:53 | IP
|
|
Legenda

Новичок
|
    
ОГРОМНОЕ СПАСИБО!
(Сообщение отредактировал Legenda 25 окт. 2009 15:39)
|
Всего сообщений: 22 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 15:36 | IP
|
|
oc


Новичок
|
     
найти угол между прямой L и плоскостью S в пространстве, если: L=x-3/0=y/-2=z+11/4 a S=3y+z-7=0
|
Всего сообщений: 8 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 16:11 | IP
|
|
respect78


Новичок
|
    
Помогите пожалуйста!!!
Дана треугольная пирамида
S (2;3;5)
A (3;-3;-2)
B (-3;3;-3)
C (-3;3;-3)
а) уравнение плоскости, проходящей через точки А, В и С;
б) величину угла между ребром SC и гранью АВС;
в) площадь грани АВС;
г) уравнение высоты, опущенной из вершины S на грань АВС и ее длину;
д) объем пирамиды SABC.
|
Всего сообщений: 3 | Присоединился: октябрь 2009 | Отправлено: 30 окт. 2009 18:35 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: respect78 написал 30 окт. 2009 18:35
Дана треугольная пирамида
S (2;3;5)
A (3;-3;-2)
B (-3;3;-3)
C (-3;3;-3)
У Вас точки B и C имеют одинаковые координаты. ТОгда это не может быть пирамидой.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 1 нояб. 2009 12:29 | IP
|
|
respect78


Новичок
|
    
У Вас точки B и C имеют одинаковые координаты. ТОгда это не может быть пирамидой.
Да ты прав, я ошибся!!!=(
С (-3;-2;-5)
|
Всего сообщений: 3 | Присоединился: октябрь 2009 | Отправлено: 2 нояб. 2009 14:13 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: respect78 написал 30 окт. 2009 18:35
Помогите пожалуйста!!!
Дана треугольная пирамида
S (2;3;5)
A (3;-3;-2)
B (-3;3;-3)
C (-3;3;-3)
а) уравнение плоскости, проходящей через точки А, В и С;
 )
 )
 )
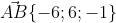

Уравнение плоскости ABC имеет вид:
|x-3 y+3 z+2| = 0
| -6 6 -1|
| -6 1 -3|
(x-3)*|6 -1| - (y+3)*|-6 -1| + (z+2)*|-6 6| = 0
|1 -3| |-6 -3| |-6 1|
(x-3)*(- 18 + 1) - (y+3)*(18 - 6) + (z+2)*(- 6 + 36) = 0
- 17(x-3) - 12(y+3) + 30(z+2) = 0
- 17x + 51 - 12y - 36 + 30z + 60 = 0
- 17x - 12y + 30z + 75 = 0
17x + 12y - 30z - 75 = 0 - уравнение плоскости ABC
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 2 нояб. 2009 15:03 | IP
|
|

 Форум
Форум

 Математика
Математика

 Аналитическая геометрия
Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 Аналитическая геометрия
Аналитическая геометрия