RKI 


Долгожитель
|
     
Цитата: respect78 написал 30 окт. 2009 18:35
б) величину угла между ребром SC и гранью АВС;
17x + 12y - 30z - 75 = 0 - уравнение плоскости ABC
a = 17; b = 12; c = -30
 )
 )
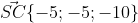
Уравнение прямой SC имеет вид:
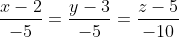
l = -5; m = -5; n = -10
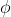 - угол между ребром SC и плоскостью ABC - угол между ребром SC и плоскостью ABC

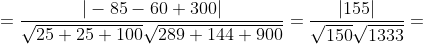
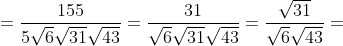
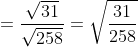
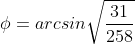
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 2 нояб. 2009 15:18 | IP
|
|
Angelina88

Новичок
|
     
Здравствуйте. Помогите пожалуйста решить тест! Я половину сделала, а это никак!! Заранее спасибо. Вот некоторые задачи:
Найти точки пересечения плоскости 2x - 3y - 4z - 24 = 0 с осями координат.
a) [ ] (2,0,0)
b) [ ] (12,0,0)
c) [ ] (0,-3,0)
d) [ ] (0,-8,0)
e) [ ] (0,0,-4)
f) [ ] (0,0,-6)
_ _
Может ли смешанное произведение векторов a, b ,c превосходить произведение длин этих векторов?
a) ( ) да
b) ( ) нет
Совокупностью каких условий определяется векторное
_ _ _
произведение c = [ a, b ] векторов a и b ?
^
_ _ _ _ _ _
a) [ ] [a, b] = I a I * I b I sin (ab)
_ _ _
b) [ ] ([ a, b ], b ) = 0
] _ _
c) [ ] тройка векторов a, b , c - правая
_ _ _
d) [ ] ([ a, b ], a ) = 0
^
_ _ _ _ _ _
e) [ ] I [ a, b] I = IaI * IbI sin (ab)
_ _ _
f) [ ] тройка векторов a, b ,c - левая
|
Всего сообщений: 2 | Присоединился: ноябрь 2009 | Отправлено: 2 нояб. 2009 15:55 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Angelina88 написал 2 нояб. 2009 15:55
Найти точки пересечения плоскости 2x - 3y - 4z - 24 = 0 с осями координат.
a) [ ] (2,0,0)
b) [ ] (12,0,0)
c) [ ] (0,-3,0)
d) [ ] (0,-8,0)
e) [ ] (0,0,-4)
f) [ ] (0,0,-6)
b); d); f)
Может ли смешанное произведение векторов a, b ,c превосходить произведение длин этих векторов?
a) ( ) да
b) ( ) нет
a)
Совокупностью каких условий определяется векторное
произведение c = [ a, b ] векторов a и b ?
^
_ _ _ _ _ _
a) [ ] [a, b] = I a I * I b I sin (ab)
_ _ _
b) [ ] ([ a, b ], b ) = 0
] _ _
c) [ ] тройка векторов a, b , c - правая
_ _ _
d) [ ] ([ a, b ], a ) = 0
^
_ _ _ _ _ _
e) [ ] I [ a, b] I = IaI * IbI sin (ab)
_ _ _
f) [ ] тройка векторов a, b ,c - левая
b); c); e)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 9:01 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: respect78 написал 30 окт. 2009 18:35
в) площадь грани АВС;
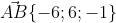

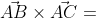
= | i j k| = i*|6 -1| - j*|-6 -1| + k*|-6 6| =
|-6 6 -1| |1 -3| |-6 -3| |-6 1|
|-6 1 -3|
= i*(- 18 + 1) - j*(18 - 6) + k*(-6 + 36) = - 17i - 12j + 30k
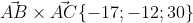
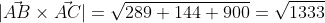
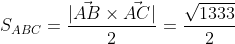
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 10:22 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: respect78 написал 30 окт. 2009 18:35
г) уравнение высоты, опущенной из вершины S на грань АВС и ее длину;
Пусть SH - высота, опущенная из вершины S на грань ABC.
Пусть уравнение высоты SH имеет вид:
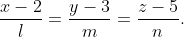
Коэффициенты l, m и n необходимо определить.
Прямая SH и плоскость ABC: 17x + 12y - 30z - 75 = 0 перпендикулярны. По условию перпендикулярности прямой и плоскости в пространстве:
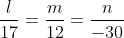

Уравнение высоты SH имет вид:
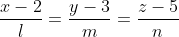
}{17n} = - \frac{30(y-3)}{12n} = \frac{z-5}{n} )
}{17} = -\frac{30(y-3)}{12} = z-5 )
Найдем координаты точки H.
Точка H(x;y;z) лежит на прямой SH. Следовательно, координаты точки H удовлетворяют уравнению прямой SH:
}{17} = - \frac{30(y-3)}{12} = z-5 = t )
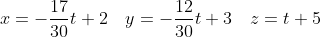
 )
С другой стороны, точка H лежит на плоскости ABC. Следовательно, координаты точки H удовлетворяют уравнению плоскости ABC:
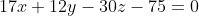
 + 12(-\frac{12}{30}t+3) - 30(t+5) - 75 = 0 )
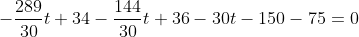


 )
 )
^{2} + (3 - \frac{69}{43})^{2} + (5 - \frac{365}{43})^{2} = \frac{7225}{1849} + \frac{3600}{1849} + \frac{22500}{1849} = \frac{775}{43} )
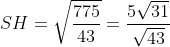
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 11:06 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: respect78 написал 30 окт. 2009 18:35
д) объем пирамиды SABC.

|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 11:08 | IP
|
|
Mila


Новичок
|
      
Всем добрый день!!! Направьте меня, пожалуйста, в нужную сторону, что-то я никак не соображу, что мне сделать нужно?
Даны координаты вершин пирамиды ABCD, A(10, 6, 6), B (-2, 8, 2), C(6, 8, 9), D (7, 10, 3). Одно из заданий: найти уравнение прямой АВ (нашла), и уравнение отрезка АВ (а вот с этим- заморочка). Как искать? И что искать?
|
Всего сообщений: 12 | Присоединился: ноябрь 2008 | Отправлено: 7 нояб. 2009 18:12 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Mila написал 7 нояб. 2009 18:12
Всем добрый день!!! Направьте меня, пожалуйста, в нужную сторону, что-то я никак не соображу, что мне сделать нужно?
Даны координаты вершин пирамиды ABCD, A(10, 6, 6), B (-2, 8, 2), C(6, 8, 9), D (7, 10, 3). Одно из заданий: найти уравнение прямой АВ (нашла), и уравнение отрезка АВ (а вот с этим- заморочка). Как искать? И что искать?
Уравнение отрезка можно записать в параметрическом виде:
{x(t) = (-2-10)t + 10; y(t) = (8-6)t + 6; z(t) = (2-6)t + 6; 0 <= t <= 1
{x(t) = - 12t + 10; y(t) = 2t + 6; z(t) = - 4t + 6; 0 <= t <= 1
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 13:54 | IP
|
|
Mila


Новичок
|
      
Спасибо огромнейшее!!!
|
Всего сообщений: 12 | Присоединился: ноябрь 2008 | Отправлено: 8 нояб. 2009 14:01 | IP
|
|
katerinka241281

Новичок
|
     
Помогите, пожайлуста. =)
Дана задача. Составить уравнения касательных к кривой y=x^2-4x. проходящих через точку А (0;-1). Сделать чертеж
|
Всего сообщений: 12 | Присоединился: ноябрь 2009 | Отправлено: 25 нояб. 2009 20:13 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Аналитическая геометрия
Аналитическая геометрия

 Форум
Форум

 Математика
Математика

 Аналитическая геометрия
Аналитическая геометрия