RKI 


Долгожитель
|
    
Цитата: Nice написал 29 авг. 2009 13:49
не знаю, как квадратный корень обозначить, т.ч. я буду просто слово корень писать и в скобочки брать подкоренное выражение
Посмотрите, пожалста, верно ли решено и если нет, помогите в решении, буду очень признательна
корень(y^2 + 1)dx=xydy
dx/x=ydy/корень(y^2 + 1)
int dx/x=unt ydy/корень(y^2 + 1)
ln |x| = arcsiny + c
ln |x| - arcsiny = c
sqrt(y^2 + 1)dx = xydy
dx/x = ydy/sqrt(y^2 + 1)
int dx/x = int ydy/sqrt(y^2 + 1)
int ydy/sqrt(y^2 + 1) = (1/2)*int d(y^2+1)/sqrt(y^2+1) =
= (1/2)*2sqrt(y^2 + 1) + const = sqrt(y^2 + 1) + const
int dx/x = int ydy/sqrt(y^2 + 1)
ln|x| = sqrt(y^2 + 1) + const
ln|x| - sqrt(y^2 + 1) = const
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 29 авг. 2009 14:56 | IP
|
|
Nice


Новичок
|
    
Пасибочки огроменное!! Вы меня просто спасли!!
|
Всего сообщений: 6 | Присоединился: август 2009 | Отправлено: 29 авг. 2009 16:53 | IP
|
|
Graf de la Kruf


Новичок
|
    
RKI скажите пожалуйста а операционный метод что из себя представляет? а то я че то не соображу?
|
Всего сообщений: 25 | Присоединился: август 2009 | Отправлено: 1 сен. 2009 13:34 | IP
|
|
Graf de la Kruf


Новичок
|
    
Найти общий интеграл ДУ высшего порядка:
y"=2*x-7*exp(x/2)
спасибо))))
|
Всего сообщений: 25 | Присоединился: август 2009 | Отправлено: 1 сен. 2009 13:50 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Graf de la Kruf написал 1 сен. 2009 13:34
RKI скажите пожалуйста а операционный метод что из себя представляет? а то я че то не соображу?
Операционный метод состоит в использовании прямого и обратного преобразования Лапласа.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 1 сен. 2009 15:02 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Graf de la Kruf написал 1 сен. 2009 13:50
Найти общий интеграл ДУ высшего порядка:
y"=2*x-7*exp(x/2)
y'' = 2x - 7exp(x/2)
y' = (x^2) - 14exp(x/2) + C
y = (1/3)(x^3) - 28exp(x/2) + Cx + D
C и D - произвольные константы
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 1 сен. 2009 15:04 | IP
|
|
sessia


Новичок
|
    
помогите, пожалуйста, решить дифференциальное уравнение:
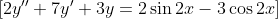
Я нашла корни характеристического уровнения k1=-1/2, k2=-3, а дальше возникли трудности, не могу решить y(одн.) и y(частн.)
(Сообщение отредактировал sessia 5 сен. 2009 14:34)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 4 сен. 2009 19:44 | IP
|
|
Benzema18


Новичок
|
       
Помогите пожалуйста.
Нужно найти общее решение дифференциального уравнения

(Сообщение отредактировал Benzema18 4 сен. 2009 22:18)
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 4 сен. 2009 21:48 | IP
|
|
attention 


Долгожитель
|
     
sessia и Benzema18, когда вставляете формулу на Форум, не забывайте пропускать строку сверху и снизу формулы, чтобы она не сливалась с текстом. Т.е.
sessia
помогите, пожалуйста, решить дифференциальное уравнение:
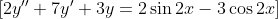
Я нашла корни характеристического уровнения k1=-1/2, k2=-3, а дальше возникли трудности, не могу решить y(одн.) и y(частн.)
Benzema18
Помогите пожалуйста.
Нужно найти общее решение дифференциального уравнения

Пожалуйста, отредактируйте свои посты!
(Сообщение отредактировал attention 4 сен. 2009 21:06)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 4 сен. 2009 22:05 | IP
|
|
Benzema18


Новичок
|
       
отредактировал
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 4 сен. 2009 22:28 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)