attention 


Долгожитель
|
     
Цитата: Benzema18 написал 4 сен. 2009 20:48
Помогите пожалуйста.
Нужно найти общее решение дифференциального уравнения

Надо разделить переменные и вычислить интегралы.



Т.е. получили решение уравнения в неявном виде.
(Сообщение отредактировал attention 4 сен. 2009 22:44)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 4 сен. 2009 23:38 | IP
|
|
sessia


Новичок
|
    
В исправленном виде: помогите, пожалуйста, решить дифференциальное уравнение:
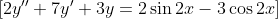
Я нашла корни характеристического уровнения k1=-1/2, k2=-3, а дальше возникли трудности, не могу решить y(одн.) и y(частн.)
(Сообщение отредактировал sessia 5 сен. 2009 14:34)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 5 сен. 2009 14:33 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Graf de la Kruf написал 27 авг. 2009 11:45
Найти частное решение линейного ДУ второго порядка, удовлетворяющее заданным начальным условиям. Задача решается дважды: классическим и операционным методами.
y"-4*y'+13*y=26*x+5; y(0)=1 y'(0)=0
заранее благодарю))))
Решение вашего уравнения операционным методом смотрите в соответсвующем разделе:
2.2.3 Операционное исчисление
(Сообщение отредактировал attention 7 сен. 2009 1:26)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 5 сен. 2009 16:09 | IP
|
|
sessia


Новичок
|
    
большое спасибо, attention, не знала про этот метод...
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 5 сен. 2009 16:27 | IP
|
|
attention 


Долгожитель
|
     
Цитата: sessia написал 5 сен. 2009 13:33
В исправленном виде: помогите, пожалуйста, решить дифференциальное уравнение:
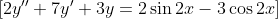
Я нашла корни характеристического уровнения k1=-1/2, k2=-3, а дальше возникли трудности, не могу решить y(одн.) и y(частн.)
Составим характеристическое уравнение и найдем его корни:

Так как корни действительны и различны, то, следовательно, общее решение соответствующего уравнения без правой части запишется так:

Так как числа  не являются корнями характеристического уравнения, то частное решение неоднородного уравнения ищем в виде: не являются корнями характеристического уравнения, то частное решение неоднородного уравнения ищем в виде:

Дважды дифференцируем:

Теперь подставим это в исходное уравнение, приравняем коэффициенты при косинусах и синусах и найдём 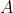 и и 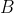 : :

Следовательно, частным решением будет функция:
 . .
А общим решением будет функция:

(Сообщение отредактировал attention 5 сен. 2009 18:35)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 5 сен. 2009 19:32 | IP
|
|
sessia


Новичок
|
    
Помогите, пожалуйста, найти общее решение дифференциального уравнения:

По дидактичке пробовала так:
x^2dy=(8xy+3y)dx , а дальше как упрощать, как интегрировать обе части так и не разобралась...
(Сообщение отредактировал sessia 8 сен. 2009 17:46)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 8 сен. 2009 17:40 | IP
|
|
attention 


Долгожитель
|
     
Цитата: sessia написал 8 сен. 2009 16:40
Помогите, пожалуйста, найти общее решение дифференциального уравнения:

По дидактичке пробовала так:
x^2dy=(8xy+3y)dx , а дальше как упрощать, как интегрировать обе части так и не разобралась...

|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 сен. 2009 18:04 | IP
|
|
sessia


Новичок
|
    
очень Вам благодарна, attention
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 8 сен. 2009 18:11 | IP
|
|
Vadim M

Новичок
|
    
Здравствуйте. Мне нужна помощь в решении системы дифференциальных уравнений второго порядка. Тема задания: численные методы, решение дифференциальных уравнений. Как следует из задания, решить систему надо не аналитически, а численно, причём каким угодно методом. Я работаю в программе Mathcad 2000 (там и решаю это). Вообще, было неплохо решить эту систему с помощью встроенной функции rkfixed (это решение уравнения или системы методом Рунге-Кутта 4-го порядка точности). Но дело в том, что для работы с этой функцией пригодны только уравнения (системы) ПЕРВОГО порядка. Собственно вопрос такой: каким образом свести эту систему к уравнениям первого порядка или без сведения решить эту систему?
Задание прикрепляется.

Заранее спасибо.
(Сообщение отредактировал Vadim M 8 сен. 2009 18:51)
(Сообщение отредактировал Vadim M 8 сен. 2009 18:53)
|
Всего сообщений: 3 | Присоединился: сентябрь 2009 | Отправлено: 8 сен. 2009 18:50 | IP
|
|
attention 


Долгожитель
|
     
Vadim M, попробуйте использовать Maple 12 или 13 (все продуманно до не могу) в нем эта система числено решается очень просто.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 сен. 2009 19:26 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)