Vadim M

Новичок
|
    
Вы знаете, мы работаем именно в маткад. У нас проходил курс "Вычислительные методы", где мы вели работу с маткад. Другое просто преподаватель не примет, да и я не знаком с этими системами (maple)
|
Всего сообщений: 3 | Присоединился: сентябрь 2009 | Отправлено: 8 сен. 2009 20:04 | IP
|
|
ProstoVasya

Долгожитель
|
    
Vadim M

|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 9 сен. 2009 9:07 | IP
|
|
pyuriy

Новичок
|
     
Здравствуйте!
помогите плиз с примером. Нужно разрешить уравнение относительно переменной z (представить в виде z=f(x,y)).
К примеру:
(x^2\9)+(y^2\4)+z^2=1
решение:
z=√1-(x^2\9)-(y^2\4)
А вот сам пример:
(x^2/4)+(y^2/9)+(z^2/4)=1
|
Всего сообщений: 1 | Присоединился: сентябрь 2009 | Отправлено: 9 сен. 2009 11:56 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: pyuriy написал 9 сен. 2009 11:56
Нужно разрешить уравнение относительно переменной z (представить в виде z=f(x,y)).
К примеру:
(x^2\9)+(y^2\4)+z^2=1
решение:
z=√1-(x^2\9)-(y^2\4)
А вот сам пример:
(x^2/4)+(y^2/9)+(z^2/4)=1
(x^2)/4 + (y^2)/9 + (z^2)/4 = 1
(z^2)/4 = 1 - (x^2)/4 - (y^2)/9
z^2 = 4 - (x^2) - 4(y^2)/9
далее выразите z
(Сообщение отредактировал RKI 9 сен. 2009 12:30)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 сен. 2009 12:22 | IP
|
|
Fist53

Новичок
|
     
Добры вечер.
У меня в пятницу пересдача математики, надо решить дифф. уравнения, а математику я практически не понимаю. Помогите пожалуйста решить примеры (любые которые не затруднит).
1.
(1+y^2)dx - y\sqrt{1-x^2}dy=0
2.
2xcos^2 ydx-(x^2-3)sin2ydy=0
3.
xy^' + y= xy^2ln x
4.
y^(6) - y^(4)=1
|
Всего сообщений: 5 | Присоединился: сентябрь 2009 | Отправлено: 9 сен. 2009 21:10 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Fist53 написал 9 сен. 2009 20:10
Добры вечер.
У меня в пятницу пересдача математики, надо решить дифф. уравнения, а математику я практически не понимаю. Помогите пожалуйста решить примеры (любые которые не затруднит).
1.


|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 10 сен. 2009 2:08 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Fist53 написал 9 сен. 2009 20:10
Добры вечер.
У меня в пятницу пересдача математики, надо решить дифф. уравнения, а математику я практически не понимаю. Помогите пожалуйста решить примеры (любые которые не затруднит).
2. 


|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 10 сен. 2009 2:48 | IP
|
|
Fist53

Новичок
|
     
спасибо большое за эти примеры
|
Всего сообщений: 5 | Присоединился: сентябрь 2009 | Отправлено: 10 сен. 2009 12:13 | IP
|
|
Fist53

Новичок
|
     
2.
y^'=\left(1+\frac{y-1}{2x}\right)^2
z=y-1
V=\frac{y-1}{x}
y-1=Vx
y'=V'x+V
V'x+V=(1+0,5V)^2
подскажите что дальше с этим сделать
(Сообщение отредактировал Fist53 10 сен. 2009 13:42)
(Сообщение отредактировал Fist53 10 сен. 2009 13:44)
(Сообщение отредактировал Fist53 10 сен. 2009 13:44)
|
Всего сообщений: 5 | Присоединился: сентябрь 2009 | Отправлено: 10 сен. 2009 13:40 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Fist53 написал 9 сен. 2009 20:10
Добры вечер.
У меня в пятницу пересдача математики, надо решить дифф. уравнения, а математику я практически не понимаю. Помогите пожалуйста решить примеры (любые которые не затруднит).
3.

Это уравнение Бернулли. Поделим обе части на 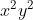 и сделаем замену. и сделаем замену.

|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 10 сен. 2009 13:51 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)