Viktori

Новичок
|
     
Помогите пожалуйста исследовать функции и простроить графики!! Прочитала кучу лекций как их строить, но понять так и не смогла((
1) y= x^3 +4 / x^2
2) y+ x^2-x+1 / x-1
3) y= 2/ x^2 +2x
4) y= 4x^2 / x^2+3
5) y= 12x / x^2+9
6) y= x^2-3x+3 / x-1
7) y= 4-x^3 / x^2
8) y= x^2-4x+1 / x-4
9) y=2x^3+1 / x^2
10) y= (x-1)^2 / X^2
Заранее всем ОГРОМНОЕ СПАСИБО!!
|
Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 22 нояб. 2009 9:29 | IP
|
|
katerinka241281

Новичок
|
     
Помогите пожалуйста исследовать функцию
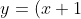e^{-x^2/4})
(Сообщение отредактировал attention 7 дек. 2009 1:22)
|
Всего сообщений: 12 | Присоединился: ноябрь 2009 | Отправлено: 24 нояб. 2009 12:03 | IP
|
|
Tommy


Новичок
|
     
Добрый вечер!
Помогите, пожалуйста, провести полное исследование функции! График я сам построю

Буду очень благодарен!
(Сообщение отредактировал attention 7 дек. 2009 1:22)
|
Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 29 нояб. 2009 20:13 | IP
|
|
natafka


Новичок
|
     
Помогите , пожалуйста, )))))) найти экстремум функции с 2-мя неизвестными.
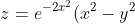)
(Сообщение отредактировал attention 6 дек. 2009 22:56)
|
Всего сообщений: 49 | Присоединился: ноябрь 2008 | Отправлено: 5 дек. 2009 19:43 | IP
|
|
STRELLA

Новичок
|
     
Будьте добры, помогите решить!!!
Представить интегралом Фурье заданную функцию y=f(x) и построить её график.

Зараннее, огромное спасибо!
(Сообщение отредактировал attention 6 дек. 2009 23:04)
|
Всего сообщений: 17 | Присоединился: ноябрь 2009 | Отправлено: 6 дек. 2009 14:37 | IP
|
|
Putnik Ada


Новичок
|
     
Подскажите, пожалуйста, как рассчитать точки для построения трехмерного графика в виде спирали ДНК.
(Сообщение отредактировал attention 7 дек. 2009 1:23)
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 6 дек. 2009 22:14 | IP
|
|
attention 


Долгожитель
|
      
Цитата: STRELLA написал 6 дек. 2009 13:37
Будьте добры, помогите решить!!!
Представить интегралом Фурье заданную функцию y=f(x) и построить её график.

Зараннее, огромное спасибо!
STRELLA, если хотите, чтобы Вам помогли, перенесите своё задание в соответствующую тему:
2.1.18 Ряд Фурье
(Сообщение отредактировал attention 6 дек. 2009 23:05)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 6 дек. 2009 23:36 | IP
|
|
Mishelka

Новичок
|
     
Добрый вечер, помогите пожалуйста вот с таким заданием...
Построить график функции y= f(x), используя общую схему исследования функции.
y = (2x-3) / (x^2 - 3x + 3).
1) Область определения функции x^2 - 3x + 3 не равно 0.
D = 9 - 12 = -3 <0 => корней нет.
D(y) = (-бесконечность; + бесконечность).
2) Функция непрерывна. Точек разрыва нет.
3) Функция общего вида. Не является ни четной ни нечетной.
4) Пересечение с осью Оx.
{y = 0 ; y = (2x - 3) / (x^2 - 3x +3) ;
(2x-3) / (x^2 - 3x +3) = 0.
2x-3 =0.
x = 1.5
M (1.5 ; 0) ;
Пересечение с осью Oy
{x = 0; y= (2x-3) / (x^2 - 3x +3) ;
{ x=0 ; y = -1 ;
M (0; -1);
5) Возрастание/ убывание функции. Экстремумы.
y' = (2* (x^2 - 3x + 3) - (2x - 3) (2x - 3) ) / (x^2 - 3x +3)^2 = ( 2 x^2 - 6x +6 - 4x^2 +12x - 9) / (x^2 - 3x + 3) ^2 = ( - 2x^2 + 6x - 3) / (x^2 -3x + 3)^2 .
y' = 0;
( - 2x^2 + 6x - 3) / (x^2 -3x + 3)^2 = 0;
( - 2x^2 + 6x - 3) = 0;
D= 36 - 24 = 12;
x1,2 = (-6 ± sqrt(12)) / -4 = (6 ± 2sqrt(3)) / 4 = (3 ± sqrt(3)) / 2 ;
x1=0, 634;
x2= 2, 366;
x1-точка минимума.
x2 - точка максимума.
6) Интервал выпуклости/ вогнутости точки перегиба.
y'' = ( (-4x + 6) (x^2 - 3x +3) ^2 - 2 (2x^2 - 3) (-2x^2 +6x - 3) ) / (x^2 -3x +3) ^4 =
= ( (-4x+6) ((x^2 - 3x +3)^2 + (-2x^2 + 6x -3)) ) / (x^2 - 3x +3)^4 .
y'' = 0 при (-4x+6) = 0 или ( (x^2 - 3x +3)^2 + (-2x^2 +6x -3) ) = 0
x = 1,5 (x^2 -3x + 3)^2 = 2x^2 -6x +3
7) асимптоты
а) вертикальные. Нет.
б) Наклонные.
k = Lim при x->бесконечности y/x = Lim при x->бесконечности (2x-3) / ((x^2 - 3x +3)x) = Lim при x->бесконечности (2x-3) / (x^3 - 3x^2 +3x) = 0;
и = Lim при x->бесконечности (y-kx) = Lim при x->бесконечности ( (2x-3)/ (x^2 - 3x +3) - 0*x ) = Lim при x->бесконечности (2x-3)/(x^2 -3x +3) = 0;
y=0 -горизонтальная асимптота.
8) график...
посмотрите пожалуйста где допустила ошибку и вообще так ли решаю... + если можно постройте график... заранее большое спасибо...
Помогите пожалуйста! Составить уравнение касательной и нормали к графику кривой y=f(x) точке, абсцисса которой равна x0.
y = sqrt (4-2x^2)
x0 = 1;
очень нужно...заранее большое спасибо...
(Сообщение отредактировал attention 10 дек. 2009 8:37)
|
Всего сообщений: 6 | Присоединился: декабрь 2009 | Отправлено: 9 дек. 2009 17:26 | IP
|
|
FoxSov


Новичок
|
      
Помогите решить задачу на экстремум, пожалуйста.
На прямоугольном отрезке АВ, соединяющем два источника света: А (силой р) и В (силой q), найти точку М ,наименее освещенную, если \АВ\ = а. Освещенность обратно пропорциональна квадрату
расстояния от источника света.
|
Всего сообщений: 7 | Присоединился: август 2009 | Отправлено: 10 дек. 2009 1:32 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Mishelka написал 9 дек. 2009 16:26
Помогите пожалуйста! Составить уравнение касательной и нормали к графику кривой y=f(x) точке, абсцисса которой равна x0.
y = sqrt (4-2x^2)
x0 = 1;
очень нужно...заранее большое спасибо...
^\prime = \frac{\left(4 - 2x^2\right)^\prime}{2\sqrt {4 - 2x^2} } = - \frac{2x}{\sqrt {4 - 2x^2} }. \hfill \\ {y'}_0 = - \frac{2x_0}{\sqrt {4 - 2x_0^2} } = - \frac{2 \cdot 1}{\sqrt {4 - 2 \cdot 1^2} } = - \frac{2}{\sqrt 2} = - \sqrt 2 . \hfill \\ \end{gathered} )
Составим уравнение нормали:
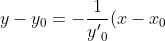 \Leftrightarrow y - \sqrt 2 = \frac{1}{\sqrt 2 }\left(x - 1\right) \Leftrightarrow y = \frac{\sqrt 2}{2}x + \frac{\sqrt 2 }{2}.)
Составим уравнение касательной:
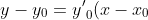 \Leftrightarrow y - \sqrt 2 = - \sqrt 2 (x - 1) \Leftrightarrow y = - \sqrt 2 x + 2\sqrt 2 .)
Смотрите график функции с нормалью и касательной.

|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 10 дек. 2009 9:42 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.4 Исследование функций одной и многих переменных
2.1.4 Исследование функций одной и многих переменных

 Форум
Форум

 Математика
Математика

 2.1.4 Исследование функций одной и многих переменных
2.1.4 Исследование функций одной и многих переменных