RKI 


Долгожитель
|
    
Цитата: Gramatonchik написал 7 марта 2010 15:01
1. Есть 2 ящика. в Одном 18 белых шаров и 4 красных, во втором 8 белых и 12 красных. Какова вероятность того, чо когда вытянут два шара, один из них будет красным?
Как достаются шарики? Из первой урны? Из второй? Из обеих (то как)?
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 марта 2010 15:45 | IP
|
|
Gramatonchik


Новичок
|
    
достают из каждой урны)
Огромное спасибо за уже предоставленные решения.
|
Всего сообщений: 3 | Присоединился: март 2010 | Отправлено: 7 марта 2010 16:33 | IP
|
|
temegve


Новичок
|
     
Здравствуйте, помогите пожалуйста решить задачу:
Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу равна 0.6, ко второму 0.4. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом равна 0.9, а вторым - 0.95. Стандартное изделие при проверке было признано стандартным. Найти вероятность того, что изделие проверил второй товаровед.
|
Всего сообщений: 11 | Присоединился: май 2009 | Отправлено: 8 марта 2010 16:27 | IP
|
|
sirena


Новичок
|
     
помогите ответить на вопрос дополнитльный...задачу решила, а вот на него ответ не нашла(
задача:на сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: 10 с первого завода, 20 со второго и 20 с третьего. Вероятность качественного изготовления изделий на 1 заводе 0,7..на 2-ом 0,9...на 3-м 0,7..какова вероятность того что взятое случайным образом изделие окажется качественным?
я решила, получилось Р(А)= 0,07*0,18*0,24-0,003024
А вот и вопрос:В условиях предыдущей задачи взятой случайным образом изделие оказалось качественным.Какова вероятность того, что оно изготовлено на 3-м заводе???
|
Всего сообщений: 7 | Присоединился: март 2010 | Отправлено: 8 марта 2010 22:52 | IP
|
|
sirena


Новичок
|
     
блин..а ведь была уверена что вычисления верны(((
Вы не поможете тогда если не трудно вот с этой задачей еще..
В магазине выставлены для продажи 19 изделий, среди которых 6 изделий некачественные. Какова вероятность того, что взятые случайным образом 3изделия будут некачественными?
(Сообщение отредактировал sirena 9 марта 2010 19:21)
|
Всего сообщений: 7 | Присоединился: март 2010 | Отправлено: 9 марта 2010 19:09 | IP
|
|
tatka111


Новичок
|
    
RKI Здраствуйте. Вы мне решали несколько задач. И когда я села за них, разбираться в решении, то возник вопрос решения следующей задачи:
В среднем 5% яблонь доживают до 170 лет. Найти вероятность того, что из 100 наудачу выбранных яблонь доживут до 170 лет:
а) 3 яблони; б) не более 5 яблонь.
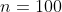 - количество яблонь - количество яблонь
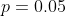 - вероятность того, что яблоня доживет до 170 лет - вероятность того, что яблоня доживет до 170 лет
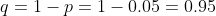
 = 5 )
*(0.95)} = \sqrt{4.75} \sim 2.1794 )
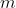 - количество яблонь, доживших до 170 лет - количество яблонь, доживших до 170 лет
а) 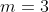
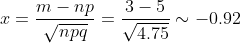
По локальной теореме Муавра-Лапласа
 = \frac{\phi (x)}{\sqrt{npq} } \sim \frac{\phi (-0.92)}{\sqrt{4.75} } = )
}{\sqrt{4.75} } \sim \frac{0.26129}{\sqrt{4.75} } \sim 0.119888 )
б) 
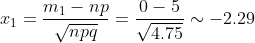
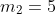
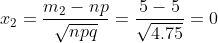
По интегральной теореме Муавра-Лапласа
 = P(m_{1} \le m \le m_{2}) = \Phi (x_{2}) - \Phi (x_{1}) = )
 - \Phi (-2.29) = \Phi (0) + \Phi (2.29) \sim 0 + 0.4893 = 0.4893 )
Согласно условиям применения т. Муавра-Лапласа:
npq больше либо равно 20
А в данной задаче npq = 4,75
Может в данном случае применима т. Пуассона?
Помогите разобраться.
|
Всего сообщений: 22 | Присоединился: октябрь 2009 | Отправлено: 10 марта 2010 17:45 | IP
|
|
RKI 


Долгожитель
|
    
tatka111
Вы можете использовать и теорему Пуассона в данном случае. Ответ получится несколько точнее.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 марта 2010 18:41 | IP
|
|
ozzy123


Новичок
|
    
ДОБРЫЙ ВЕЧЕР!!!Задачка следующая:
Три охотника ведут огонь по кабану. Вероятность попадания в цель для первого охотника равна 0,72; для второго-0,81; а для третьего-0,78. Какова вероятность, что кабан будет убит, если для этого достаточно 2-х попаданий, а у каждого охотника осталось по одному патрону?
Заранее спасибо=)
|
Всего сообщений: 1 | Присоединился: март 2010 | Отправлено: 10 марта 2010 19:00 | IP
|
|
Alexander91

Новичок
|
    
Здравствуйте, помогите пожалуйста решить две задачи:
1. Определить вероятность того, что выбранное наудачу изделие является первосортным, если известно, что 4% всей продукции составляет брак, а 75% доброкачественных изделий является первосортным.
2. Вероятности того, что нужная сборщику деталь находиться в первом, втором, третьем ящиках соответственно равны: 0.6; 0.7; 0.9; Найти вероятность того, что деталь содержится не более чем в двух ящиках.
|
Всего сообщений: 1 | Присоединился: март 2010 | Отправлено: 10 марта 2010 20:11 | IP
|
|
Yulusik

Новичок
|
     
Здравствуйте, помогите пожалуйста, очень надо! Заранее благодарна!!
1.Пусть X1, X2,...,Xn - независимые, одинаково распределенные случайные величины, имеющие плотность распределения f(x)=2-2x , x принадлежит [0,1] . Найти функцию распределения случайной величины Nn=max {X1,X2,...,Xn}. Найти предел по распределению последовательности величин Nn .
2.Дана выборка X1,X2,...,Xn из генеральной совокупности, распределенной по закону Бернулли с неизвестным параметром p. Проверить, что X1, X1X2 являются несмещенными оценками соответственно для p, p^2 . Являются ли эти оценки состоятельными?
3.Дана выборка X1,X2,...,Xn из генеральной совокупности, имеющей непрерывное распределение с плотностью
fx1(x)={e^(тета-x) , при x>тета
{0, при x<тета
(где тета принадлежит (- бесконечность; +бесконечность) - неизвестный параметр). Проверить, является ли оценка состоятельной и несмещенной оценкой параметра тета.
4.Пусть X1,X2,...,Xn выборка из генеральной совокупности, распределенной по нормальному закону N(a,сигма^2), где параметр a известен, а параметр сигма^2 неизвестен. Найти оценку параметра сигма^2 по методу моментов (по второму моменту). Проверить состоятельность и несмещенность полученной оценки.
5.Пусть X1,X2,...,Xn выборка из генеральной совокупности равномерно распределенной на отрезке [тета;тета+5] , где тета - неизвестный параметр. Найти оценку параметра по методу максимального правдоподобия. Проверить состоятельность и несмещенность полученных оценок.
6.Пусть X1,X2,...,Xn выборка из генеральной совокупности, равномерно распределенной на отрезке [1;тета+2] , где тета>-1 - неизвестный параметр. Сравнить в среднеквадратичном оценки параметра метода моментов (по первому моменту) - тета1* и метода максимального правдоподобия - тета2* .
|
Всего сообщений: 21 | Присоединился: сентябрь 2009 | Отправлено: 11 марта 2010 13:02 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Теория вероятности - задачи и решения
Теория вероятности - задачи и решения

 Форум
Форум

 Математика
Математика

 Теория вероятности - задачи и решения
Теория вероятности - задачи и решения