Форум - 2.1.6 Первообразная (неопределенный интеграл) [35]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика 2.1.6 Первообразная (неопределенный интеграл)
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 ]
Модераторы: Roman Osipov, RKI, attention, paradise

Reshalka

Новичок
((cos(2x)^2)dx)/sin(2x)=((1-sin(2x)^2)dx)/sin(2x) =
=1/sin(2x)-sin(2x)
интеграл ((cos(2x)^2)dx)/sin(2x)=integral(1/sin(2x))-int(sin(2x))=
=integral(1/sin(2x))+(cos(2x))/2
int(1/sin(2x)dx)=int (sin(x)/2sin^2(x)cos(x)dx)=
=int(-1/2*ctg(x)) * d(ctg(x))=(-ln(ctg(x)))/2 или ln(tg(x))/2
ответ (ln(tg(x))+(cos(2x)))/2.

Всего сообщений: 15 | Присоединился: февраль 2010 | Отправлено: 9 фев. 2010 17:38 | IP

Reshalka

Новичок

Цитата: swanvl написал 2 фев. 2010 17:30
Помогите,
уже неделю бьюсь... Что только не пробовала.
int 1/(x^6+1)^1/2

Методом Чебышева для биномин. выражение. (x^m)*(a+b*x^n)^p
m=0 n=6 p=-1/2
1. p не целое
2. (m+1)/n не целое
3. (m+1)/n+p не целое
если не удовл. хотя бы одному услов. то не выраж. через эле. функц. ваш интеграл или так просто не берется
док. Чебышевым.

(Сообщение отредактировал Reshalka 9 фев. 2010 17:11)

Всего сообщений: 15 | Присоединился: февраль 2010 | Отправлено: 9 фев. 2010 17:57 | IP

Dmitry28

Новичок
спасибо

Всего сообщений: 16 | Присоединился: февраль 2009 | Отправлено: 9 фев. 2010 22:31 | IP

Tanusha Senina

Новичок
Нужна ваша помощь!! Помогите решить пожалуйста!!

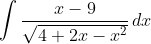
1. $\int \frac{x - 9}{\sqrt{4 + 2x - x^2}}\,dx$

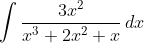
2. $\int \frac{3x^2}{x^3 + 2x^2 + x}\,dx$

3. $\int \frac{dx}{5 + 3\cos x}$

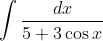
Зарание спасибо!!!

(Сообщение отредактировал attention 11 фев. 2010 14:37)

Всего сообщений: 3 | Присоединился: февраль 2010 | Отправлено: 11 фев. 2010 9:30 | IP

Tanusha Senina

Новичок
Спасибо огромнейшее!!!

Всего сообщений: 3 | Присоединился: февраль 2010 | Отправлено: 11 фев. 2010 20:12 | IP

TicTac

Новичок
аааа ппц помогите пожалуйста решить 2 интеграла ваше не в какую не могу а сроки поджимают ппц

$\int \frac{x^2-1}{\left(x^2+1\right) \sqrt{x^4+1}} \, dx$

$\int \frac{\sin{x}}{\sqrt{2+\sin{2x}}} \, dx$

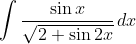
Заранее спасибо!

(Сообщение отредактировал attention 21 фев. 2010 13:55)

Всего сообщений: 6 | Присоединился: февраль 2010 | Отправлено: 13 фев. 2010 17:41 | IP

ProstoVasya

Долгожитель
1. Можно выполнить замену x = tg(t). Потом всё выразить через sin(2t).
2. Можно использовать подстановку t = tg(x). Затем подстановка Эйлера.

Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 15 фев. 2010 19:06 | IP

Mathcad

Новичок
Как можно решить такой интеграл?

В книге "Г.И. Запорожец - Руководство к решению задач по математическому анализу" есть решение этого интеграла

Но я из этого рещения вообще нечего не понял (может можно как-то по другому такие интегралы брать?

(Сообщение отредактировал attention 21 фев. 2010 13:54)

Всего сообщений: 12 | Присоединился: июнь 2009 | Отправлено: 16 фев. 2010 17:03 | IP

RKI

Долгожитель
Mathcad

Вами написано самое оптимальное и, на мой взгляд, самое доступное решение

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 17 фев. 2010 12:42 | IP

MorfMurom

Новичок
Помогите пожалуйста.

$\int\frac{\sin x+\cos x}{\cos^2x}\,dx$

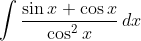
(Сообщение отредактировал attention 21 фев. 2010 13:49)

Всего сообщений: 1 | Присоединился: февраль 2010 | Отправлено: 17 фев. 2010 20:20 | IP

Отправка ответа:

Имя пользователя Вы зарегистрировались?
Пароль Забыли пароль?
Сообщение
Использование HTML запрещено
Использование IkonCode разрешено
Смайлики разрешены

Опции отправки
Добавить подпись?
Получать ответы по e-mail?
Разрешить смайлики в этом сообщении?
Просмотреть сообщение перед отправкой? Да Нет

Переход к теме
<< Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 ]