nata1717
Новичок
|
    
ProstoVasya, помогите, пожалуйста! Я правильно рассуждаю по поводу этой задачи?
Первый игрок бросает 3,а второй 2 одинаковые монеты. Выигрывает и получает все 5 монет тот , у которого большее число гербов. В случае ничьей игра повторяется до получения определённого результата. Каково мат. ожидание для каждого из игроков?
Случ. вел.Х- выигрыш первого игрока, может принимать значения -3 и 2. Вероятность того что Х=-3 находим по формуле Бернулли =Р3(0)Р2(1)+Р3(0)Р2(2)+Р3(1)Р2(2)=3/16 и плюс вероятность ничьей/2?;
Аналогично нахожу вероятность выигрыша Р(Х=2)= Р3(3)Р2(0)+Р3(3)Р2(1)+Р3(3)Р2(2)+Р3(2)Р2(0)+Р3(2)Р2(1)+Р3(1)Р2(0)=1/2 и плюс вероятность ничьей/2?
Вероятность ничьей/2 =(1-3/16-1/2)/2 =5/32
Таким образом Р(Х=-3) = 3/16+5/32=11/32,
Р(Х=2) = 1/2+5/32=21/32 ?
Аналогично для второго игрока.
Пожалуйста! Надо до среды!
|
Всего сообщений: 2 | Присоединился: март 2010 | Отправлено: 29 марта 2010 17:00 | IP
|
|
Dashul
Новичок
|
Добрый вечер
Помогите, пожалуйста, решить задачу: В первой урне находятся 5 белых и 3 красных шара, во второй - 4 белых и 2 синих. Из каждой урны вынимают по 2 шара, Х - число белых шаров в выбранных четырех. Найти распределение случайной величины Х.
Вроде бы, должна использоваться формула Бернулли... Но смущает то, что урны 2 и по 2 шара вытаскивают... Совсем запуталась( Спасибо заранее)
|
Всего сообщений: 1 | Присоединился: март 2010 | Отправлено: 29 марта 2010 23:09 | IP
|
|
Mathnet
Новичок
|
Добрый вечер.
Подскажите, пожалуйста, как решить задачу. Понимаю, что все просто, но не могу сообразить. Хотя бы с чего начать.
задача
Количество энергии, потребляемое посёлком в течение суток является случайной величиной, математическое ожидание которой равно 4тыс кв. Оценить вероятность того, что в ближайшие сутки потребление энергии:
А) превысит 8 тыс
Б)не превысит 6 тыс.
Спасибо.
(Сообщение отредактировал Mathnet 31 марта 2010 22:42)
|
Всего сообщений: 1 | Присоединился: март 2010 | Отправлено: 31 марта 2010 20:42 | IP
|
|
katbka2512
Новичок
|
Помогите пожалуйста решить задачку.
Производится выборочный контроль партии электролампочек для определния средней продолжительности их горения. Каким должен быть объем выборки, чтобы с вероятностью, не меньшей 0,9876, можно было утверждать, что средняя продолжительность эксплуатации лампочки по всей партии отклонилась от средней, полученной в выборке, не более чем на 10 часов, если среднее квадратичное отклонение продолжительности эксплуатации равно 80 часов?
Заранее спасибо
(Сообщение отредактировал katbka2512 1 апр. 2010 20:20)
|
Всего сообщений: 1 | Присоединился: апрель 2010 | Отправлено: 1 апр. 2010 20:19 | IP
|
|
Bred9tinko
Новичок
|
Все кроме этой решил....:
12 рабочих получили путевки в 4 дома отдыха: 3 - в первый, 3 - во второй, 2 - в третий, 4- в четвертый. Какова вероятность того что трое определенных рабочих попадут в один дом отдыха.
помогите плизззз
(Сообщение отредактировал Bred9tinko 3 апр. 2010 13:28)
|
Всего сообщений: 2 | Присоединился: апрель 2010 | Отправлено: 1 апр. 2010 21:07 | IP
|
|
dennokia
Новичок
|
Помогите пожалуйста решить следующую задачу:
Из колоды в 36 карт последовательно наугад вынимаются и не возвращаются 2 карты. Какова вероятность того, что оба раза извлекались карты красной масти?
|
Всего сообщений: 1 | Присоединился: апрель 2010 | Отправлено: 2 апр. 2010 17:00 | IP
|
|
attention 
Долгожитель
|
Цитата: dennokia написал 2 апр. 2010 17:00
Помогите пожалуйста решить следующую задачу:
Из колоды в 36 карт последовательно наугад вынимаются и не возвращаются 2 карты. Какова вероятность того, что оба раза извлекались карты красной масти?
Вроде так:
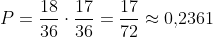
(Сообщение отредактировал attention 2 апр. 2010 19:34)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 2 апр. 2010 19:33 | IP
|
|
KB
Новичок
|
Пожалуйста помогите решить 3 задачи
1) В ящике имеется 45 деталей. Из них на первом станке изготовлено 12 деталей, на втором 15 деталей и на третьем 18 деталей. Для сборки узла детали вынимаются из ящика последоввательно одна за другой. Какова вероятность того, что во второй раз будет извлечена деталь, изготовленная на третьем станке.
2) В колоде 36 карт. Берется 5 карт. Найти вероятность того, что они пики.
3) Вероятность наступления события при одном испытании равна 0,25. С помощью формул Лапласа найти вероятность того, что при 300 испытаниях событие наступит а) 78 раз; б) не более 78 раз.
|
Всего сообщений: 3 | Присоединился: апрель 2010 | Отправлено: 3 апр. 2010 14:00 | IP
|
|
Vasilisa
Новичок
|
Помогите пожалуйста решить задачу. Никак не получается.
90% электроламп перегорают после 800 часов работы. Найти вероятность того, что электролампа перегорит в промежутке от 100 до 200 часов работы. Считать переменную времени исправной работы распределенной по показательному закону распределения.
(Сообщение отредактировал Vasilisa 5 апр. 2010 18:44)
|
Всего сообщений: 31 | Присоединился: февраль 2009 | Отправлено: 3 апр. 2010 18:15 | IP
|
|
JuliettaLusia2
Новичок
|
 
Пожалуйста,помогите с решением этих задач...
1)А и Б стреляют в тире, но у них есть только один шестизарядный револьвер с одним патроном. Поэтому они договорились по очереди случайным образом крутить барабан и стрелять. Начинает А. Найдите вероятность того, что выстрел произойдет, когда револьвер будет у А.
2)Прибор может собираться из высококачественных деталей и из деталей обычного качества. В общем 40% приборов собираются из высококачественных деталей. Если прибор создан из высококачественных деталей, то его надежность (вероятность безотказной работы за время t) равна 0,95; если из деталей обычного качества – 0,7.
а) Какова вероятность безотказной работы прибора?
б) Найти вероятность того, что прибор собран из высококачественных деталей, если он испытывался в течение времени t и работал безотказно.
|
Всего сообщений: 2 | Присоединился: апрель 2010 | Отправлено: 4 апр. 2010 13:47 | IP
|
|
|
Форум
Теория вероятности - задачи и решения
