ProstoVasya

Долгожитель
|
    
inl
Ищите решение уравнения в параметрической форме:
y' = t
y=arcsin(t)+ln(1+t^2)
Исходя из
dy = y'dt
получим дифференциальное уравнение для x= x(t)
(1/sqrt(1-t^2) +t/(1+t^2))dt = tdx
Отсюда
x(t) = ln(t/(1+sqrt(1-t^2))) + arctgt +C
y=arcsin(t)+ln(1+t^2)
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 6 дек. 2009 10:20 | IP
|
|
STRELLA

Новичок
|
    
Спасибо большое "Долгожитель" за решения, немного запутанно, но я разобрался.
Если не сложно, помоги ещё, пожалуйста.
Решить систему диф.уравнений двумя способами:1. сведением к диф.уравнению высшего порядка.
2. с помощью характеристического уравнения (X*, y* - производные функций X, Y по аргументу t).
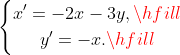
(Сообщение отредактировал attention 14 дек. 2009 0:12)
|
Всего сообщений: 17 | Присоединился: ноябрь 2009 | Отправлено: 6 дек. 2009 14:28 | IP
|
|
kruk

Новичок
|
    
Всем привет! помогите пожалуйста решить уравнение
y''=a*e^(-y'), тут нужно понизить порядок но я не пойму как. и еще не знаю что делать с e^(-y'), заранее спасибо, если можно опишите словесно что нужно сделать чтобы его решить
|
Всего сообщений: 5 | Присоединился: декабрь 2009 | Отправлено: 7 дек. 2009 16:54 | IP
|
|
attention 


Долгожитель
|
     
Цитата: kruk написал 7 дек. 2009 15:54
Всем привет! помогите пожалуйста решить уравнение
y''=a*e^(-y'), тут нужно понизить порядок но я не пойму как. и еще не знаю что делать с e^(-y'), заранее спасибо, если можно опишите словесно что нужно сделать чтобы его решить
kruk, умножьте обе части уравнения на 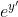 и слева у Вас получится производная и слева у Вас получится производная 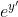 , т.е. , т.е. ^') . .
Если не понятно, смотрите полное решение:
^\prime } = a \, \Leftrightarrow \, e^{y'} = ax + C_1 \, \Leftrightarrow \hfill \\ \Leftrightarrow \, y' = \ln \left(ax + C_1\right) \, \Leftrightarrow \, y = \int \ln \left( ax + C_1 \right)dx=\left\{ \begin{gathered} ax + C_1 = t, \hfill \\ dx = \frac{dt}{a} \hfill \\ \end{gathered} \right\} = \hfill \\ = \frac{1}{a}\int {\ln t \, dt} = \frac{t}{a}\ln t - \frac{1}{a}\int {t\,d(\ln t)} = \frac{t}{a}\ln t - \frac{1}{a}\int {dt} = \hfill \\ \end{gathered})
 - \frac{ax + C_1}{a} + C_2 = \hfill \\ = \left(x + \frac{C_1}{a}\right)\ln \left(ax +a \frac{C_1}{a}\right) - \left(x + \frac{C_1}{a}\right) + C_2 = \hfill \\ = \left(x + C_1\right)\ln \left(ax + aC_1\right) - \left(x + C_1\right) + C_2. \hfill \\ \end{gathered})
Ответ:
\ln \left(ax + aC_1\right) - \left(x + C_1\right) + C_2. )
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 7 дек. 2009 17:53 | IP
|
|
kruk

Новичок
|
    
attention -спасибо тебе огромное, выручил очень)
Извините за наглость, помогите в решении еще одного (последнего) уравнения:
e^(-y)dx-(2y+x*e^(-y))dy=0
Подскажите, пожалуйста, что нужно сделать с этим уравнением чтобы решить его.
(Сообщение отредактировал attention 7 дек. 2009 18:35)
|
Всего сообщений: 5 | Присоединился: декабрь 2009 | Отправлено: 7 дек. 2009 17:58 | IP
|
|
attention 


Долгожитель
|
     
Цитата: kruk написал 7 дек. 2009 17:38
извените за наглость, помогите в решении еще одного(последнего) уравнения:
e^(-y)dx-(2y+x*e^(-y))dy=0
подскажите пожалуйста что нужно сделать с этим уравнением чтобы решить его
kruk, поделите обе части уравнения на 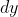 и решайте уравнение относительно функции и решайте уравнение относительно функции ) : :
 dy = 0 \, \Leftrightarrow \, e^{-y}x' - 2y - xe^{-y} = 0 \, \Leftrightarrow \, \hfill \\ \Leftrightarrow \, e^{-y}x' - xe^{-y} = 2y \, \Leftrightarrow \, e^{-y}x' + x{\left(e^{-y}\right)^\prime } = 2y \, \Leftrightarrow \hfill \\ \Leftrightarrow \, {\left(e^{-y}x\right)^\prime }_x = 2y \, \Leftrightarrow \, e^{-y}x = y^2 + C \, \Leftrightarrow \, x = \left(y^2 + C\right){e^y}. \hfill \\ \end{gathered})
(Сообщение отредактировал attention 7 дек. 2009 18:02)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 7 дек. 2009 18:58 | IP
|
|
kruk

Новичок
|
    
спасибо огромное, извените нарушения)
|
Всего сообщений: 5 | Присоединился: декабрь 2009 | Отправлено: 7 дек. 2009 19:28 | IP
|
|
Q2


Новичок
|
    
Помогите решить, пожалуйста:


Большое спасибо!
|
Всего сообщений: 10 | Присоединился: декабрь 2009 | Отправлено: 7 дек. 2009 20:53 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Q2 написал 7 дек. 2009 19:53
Помогите решить, пожалуйста:

Большое спасибо!
^\prime = - \frac{1}{x} \, \Leftrightarrow \hfill \\ \Leftrightarrow \, xy = - \ln|x| + C = - \ln|Cx| \, \Leftrightarrow \, y = - \frac{\ln|Cx}{x}. \hfill \\ \end{gathered})
Цитата: Q2 написал 7 дек. 2009 19:53
Помогите решить, пожалуйста:

Большое спасибо!
 \, \Leftrightarrow \, 2x^3y' = 2x^2y - y^3 \, \Leftrightarrow \hfill \\ \Leftrightarrow \, \frac{2x^3y'}{y^3} = \frac{2x^2}{y^2} - 1 \, \Leftrightarrow \, \frac{2x^2}{y^2} - \frac{2x^3y'}{y^3} = 1 \, \Leftrightarrow \, \frac{2x}{y^2} - \frac{2x^2y'}{y^3} = \frac{1}{x} \, \Leftrightarrow \hfill \\ \Leftrightarrow \, \frac{\left(x^2\right)^\prime}{y^2} + {x^2}{\left(\frac{1}{y^2} \right)^\prime } = \frac{1}{x} \, \Leftrightarrow \, \left( \frac{x^2}{y^2} \right)^\prime = \frac{1}{x} \, \Leftrightarrow \, \frac{x^2}{y^2} = \ln|Cx| \, \Leftrightarrow \hfill \\ \Leftrightarrow \, {y^2} = \frac{x^2}{\ln|Cx|} \, \Leftrightarrow \, y = \pm \frac{x}{\sqrt{\ln|Cx|} }. \hfill \\ \end{gathered})
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 7 дек. 2009 22:00 | IP
|
|
inl

Новичок
|
     
ProstoVasya,
спасибо огромное за помощь
|
Всего сообщений: 4 | Присоединился: декабрь 2009 | Отправлено: 7 дек. 2009 23:11 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)