attention 


Долгожитель
|
     
Для Work2008

|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 дек. 2009 3:56 | IP
|
|
attention 


Долгожитель
|
     
Цитата: STRELLA написал 6 дек. 2009 13:28
Спасибо большое "Долгожитель" за решения, немного запутанно, но я разобрался.
Если не сложно, помоги ещё, пожалуйста.
Решить систему диф.уравнений двумя способами:
1) сведением к диф.уравнению высшего порядка;
2) с помощью характеристического уравнения (X*, y* - производные функций X, Y по аргументу t).
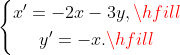
Решение первым способом (сведением к диф.уравнению высшего порядка):
 = {C_1}{e^{ - 3t} } + {C_2}{e^t}, \hfill \\y\left( t \right) = \frac{C_1}{3}{e^{ - 3t} } - {C_2}{e^t}. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered})
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 дек. 2009 17:35 | IP
|
|
Q2


Новичок
|
    
Помогите, пожалуйста! Решать начал, но как продолжить, не знаю:
Найти общее решение дифф. уравнения второго порядка. Выделить из общего решения частное, удовлетворяющее начальным условиям 

Решение:



Общее решение однородного уравнения: 
Подскажите пожалуйста, как продолжить, и правильно ли начал решать.
Большое спасибо!
(Сообщение отредактировал Q2 18 дек. 2009 19:43)
|
Всего сообщений: 10 | Присоединился: декабрь 2009 | Отправлено: 8 дек. 2009 19:34 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Q2 написал 8 дек. 2009 18:34
Помогите, пожалуйста! Решать начал, но как продолжить, не знаю:
Найти общее решение дифф. уравнения второго порядка. Выделить из общего решения частное, удовлетворяющее начальным условиям 

Решение:



Общее решение однородного уравнения: 
Подскажите пожалуйста, как продолжить, и правильно ли начал решать.
Большое спасибо!
Q2, да, начал все все правильно.

Всё понятно?
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 дек. 2009 21:52 | IP
|
|
Q2


Новичок
|
    
Огромное спасибо, attention! Все понятно! Так же понятно, что сам бы разбирался еще долго и, вероятно, не раз бы запутался 
P.S: Отдельное огромное спасибо за интегралы!
Помогите, пожалуйста!
Найти общее решение дифф. уравнения второго порядка. Выделить из общего решения частное, удовлетворяющее начальным условиям 

Решать начал аналогично предыдущему:


Но это характеристическое уравнение не имеет корней. Подскажите, каким образом решать в данном случае?
Большое спасибо!
(Сообщение отредактировал attention 23 дек. 2009 7:11)
|
Всего сообщений: 10 | Присоединился: декабрь 2009 | Отправлено: 8 дек. 2009 22:52 | IP
|
|
irishka888

Новичок
|
    
Ребята, помогите, пожалуйста, с задачами:
1. Решить дифференциальное уравнение: y'=(y-5)(8x+1)
2. Решить задачу Коши: y'=-15x^2-4x-3, y(0)=-3
Очень нужно!Заранее большое спасибо!
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 9 дек. 2009 22:05 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Q2 написал 9 дек. 2009 17:10
Помогите, пожалуйста!
Найти общее решение дифф. уравнения второго порядка. Выделить из общего решения частное, удовлетворяющее начальным условиям 

Решать начал аналогично предыдущему:


Но это характеристическое уравнение не имеет корней. Подскажите, каким образом решать в данном случае?
Большое спасибо!
 + C_2\sin(\sqrt 3 x). \hfill \\ y_2 = A\cos 3x \Rightarrow y' = - 3A\sin 3x \Rightarrow y'' = - 9A\cos 3x. \hfill \\ - 9A\cos 3x + 3A\cos 3x = 2\cos 3x \Leftrightarrow - 3A\cos 3x=\cos 3x \Rightarrow A = - \frac{1}{3}. \hfill \\ y = y_1 + y_2 = C_1\cos(\sqrt 3 x) + C_2\sin(\sqrt 3 x) - \frac{1}{3}\cos 3x. \hfill \\ \end{gathered})
Цитата: irishka888 написал 9 дек. 2009 21:05
Ребята, помогите, пожалуйста, с задачами:
1. Решить дифференциальное уравнение: y'=(y-5)(8x+1)
2. Решить задачу Коши: y'=-15x^2-4x-3, y(0)=-3.
Очень нужно!Заранее большое спасибо!
1. irishka888, разделите переменные и интегрируйте:
(8x + 1) \, \Leftrightarrow \, \frac{dy}{dx} = (y - 5)(8x + 1) \, \Leftrightarrow \hfill \\ \Leftrightarrow \, \frac{dy}{y - 5} = (8x + 1)dx \, \Leftrightarrow \, \int {\frac{dy}{y - 5} } = \int {(8x + 1)dx} \, \Leftrightarrow \hfill \\ \Leftrightarrow \, \ln|y - 5| = 4x^2 + x + C \, \Leftrightarrow \, |y - 5| = Ce^{4x^2 + x} \, \Leftrightarrow \hfill \\ \Leftrightarrow \, \left[ \begin{gathered}y_1 - 5 = Ce^{4x^2 + x}, \hfill \\- y_2 + 5 = Ce^{4x^2 + x}; \hfill \\ \end{gathered} \right. \, \Leftrightarrow \, \left[ \begin{gathered}y_1 = 5 + Ce^{4x^2 + x}, \hfill \\y_2 = 5 - Ce^{4x^2 + x}. \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered})
2. irishka888, также разделите переменные и интегрируйте, затем с учетом начального условия найдите С:
 = - 3. \hfill \\ y' = - 15x^2 - 4x - 3 \, \Leftrightarrow \, dy = \left(- 15x^2 - 4x - 3\right)dx \, \Leftrightarrow \hfill \\ \Leftrightarrow \, \int {dy} = \int {\left(-15x^2 - 4x - 3\right)dx} \, \Leftrightarrow \, y = - 5x^3 - 2x^2 - 3x + C. \hfill \\ y(0) = C - 5 \cdot 0 - 2 \cdot 0 - 3 \cdot 0 = - 3 \, \Leftrightarrow \, C = - 3. \hfill \\ \boxed{y = - 5x^3 - 2x^2 - 3x - 3} \hfill \\ \end{gathered})
(Сообщение отредактировал attention 10 дек. 2009 6:03)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 9 дек. 2009 22:39 | IP
|
|
irishka888

Новичок
|
    
attention, спасибо за решения! ;-)
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 10 дек. 2009 9:04 | IP
|
|
PoopsiK


Новичок
|
     
Очень прошу решите пожалуйста уравнения((((болела а теперь зачет не получить(((((((
1. (x^2+y^2+xy)dx=x^2dy
2.y'+2/x*y=x^3, y(1)=-5/6
3.y''+2y'+5y=e^x(9x+15)
4.y''+y=2cos7x-3sin7x
5.y'=(x+2y)/(2x-y)
6. y'-(2x-5)/x^2*y=5, y(2)=4
7. y''-2y=e^2x
8. y''+2y'+5y=-17sin2x
|
Всего сообщений: 9 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 12:24 | IP
|
|
Trushkov

Долгожитель
|
       
Вероятно, весь семестр болела...
|
Всего сообщений: 273 | Присоединился: январь 2006 | Отправлено: 11 дек. 2009 20:29 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)